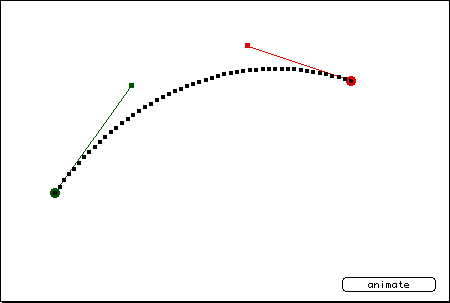

A cubic Bezier curve is defined by four points. Two are endpoints. (x0,y0) is the origin endpoint. (x3,y3) is the destination endpoint. The points (x1,y1) and (x2,y2) are control points.
Two equations define the points on the curve. Both are evaluated for an arbitrary number of values of t between 0 and 1. One equation yields values for x, the other yields values for y. As increasing values for t are supplied to the equations, the point defined by x(t),y(t) moves from the origin to the destination. This is how the equations are defined in Adobe's PostScript references.
x(t) = axt3 + bxt2 + cxt + x0
x1 = x0 + cx / 3
x2 = x1 + (cx + bx) / 3
x3 = x0 + cx + bx + axy(t) = ayt3 + byt2 + cyt + y0
y1 = y0 + cy / 3
y2 = y1 + (cy + by) / 3
y3 = y0 + cy + by + ay
This method of definition can be reverse-engineered so that it'll give up the coefficient values based on the points described above:
cx = 3 (x1 - x0)
bx = 3 (x2 - x1) - cx
ax = x3 - x0 - cx - bxcy = 3 (y1 - y0)
by = 3 (y2 - y1) - cy
ay = y3 - y0 - cy - by
Now, simply by knowing coördinates for any four points, you can create the equations for a simple Bézier curve.