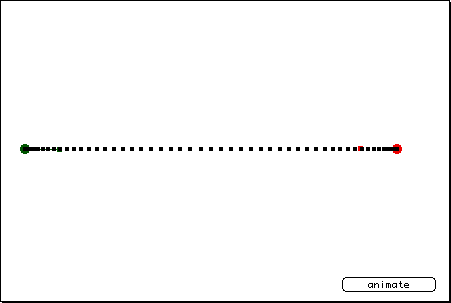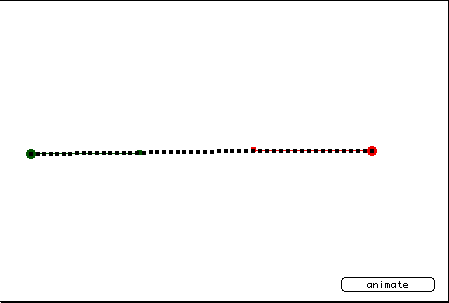

This example shows a straight line animation using a Bézier curve. As you can see, the control points lie approximately 1/3 of the distance from their associated endpoint to the other endpoint. This creates a smooth movement from origin to destination. It would probably be simpler to animate this movement with another method, though.
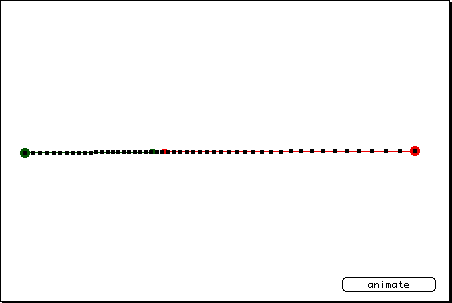
This animation, on the other hand, might be a little bit harder. As you can see from the spacing of the iterated points, the dot starts moving, slows down, then speeds up to twice its previous speed before stopping. If you look closely, you'll see that the green and red control points are almost touching, about 1/3 of the way from the origin to the destination.
Bézier curve equations are constructed in such a way that when the value for t is 0.333...., the most influential of the four defining points will be x1,y1. Likewise, at 0.666..., x2,y2 will hold sway.
Because of their (dare I say it?) flexibility, Bézier's equations are ideal for creating smoothly animated acceleration and deceleration sequences, as well as semi-complex curves.